Álvaro de Garda, uno de los 32.768 abuelos que han tenido mis nietos desde 1575
ZAS

En los libros parroquiales de Rus estaba la partida bautismal de un antepasado de la decimosexta generación
25 may 2024 . Actualizado a las 05:00 h.En los libros parroquiales de Santa María de Rus, en el Ayuntamiento de Carballo, tenemos esta partida bautismal de Juan de Garda: «A veinte y dos de abril bauticé a Juan, hijo de Álvaro de Garda y Teresa, su mujer, fueron compadres Juan de Faxín y Catalina de (¿?). Rubricado, Prado».
El año lo ponían en el centro de la hoja, y así valía para todo el ejercicio. El abuso de abreviaturas en aquellos tiempos obliga, en muchos casos, a dejar sin transcribir alguna palabra, pero en este caso, el nombre de Juan está bien transcrito, ya que así figura en las partidas bautismales de sus hijos.
Escribiendo un artículo sobre los árboles genealógicos de Romar y Garda, me vino a la memoria una leyenda que leí una vez en un libro sobre el ajedrez.
Decía la leyenda que el viejo inventor de este juego, hace muchísimos años en la India, se lo enseñó a un rey de aquel país, y este, entusiasmado por el mismo, le dijo al anciano que en recompensa por su creación le daría lo que le pidiese. El viejo sabio le respondió que no quería joyas ni riquezas, y que le bastaba simplemente con que le diese el trigo que resultara de colocar un grano en la primera casilla del tablero, el doble en la siguiente (es decir, dos granos), el doble en la siguiente (cuatro granos), y así hasta completar las 64 casillas del tablero.
El rey, pensando que con un pequeño saco de trigo saldaría su deuda, accedió. Pero cuando se puso a la tarea, se dio cuenta de que ni con todo el trigo de todas las cosechas de la India podría alcanzar para cubrir todas las casillas del tablero de ajedrez.
Efectivamente, es una mera cuestión matemática, resultado de aplicar una progresión geométrica, pero que no deja de resultar sorprendente. Curiosamente la misma fórmula matemática que se aplicaría para calcular el número de antepasados que nos corresponden a cada uno.
Así, y por la misma progresión geométrica, todos tendríamos dos padres, cuatro abuelos, ocho bisabuelos, dieciséis tatarabuelos, treinta y dos trastatarabuelos… Y si continuamos la progresión tenemos este resultado:
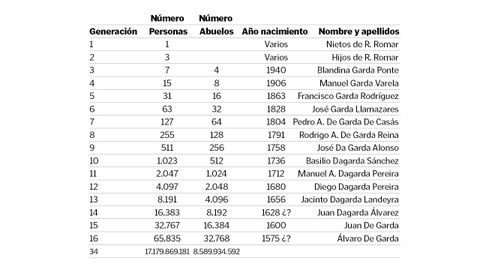
Así, el antepasado más antiguo que localicé de mi mujer Blandina, —Álvaro de Garda, padre de Juan junto a Teresa—, sería uno de los 8.192 abuelos y abuelas, y siguientes apelativos, que correspondería a la decimocuarta generación.
La misma persona, en el caso de mis nietos —es decir, dos generaciones más—, se correspondería con uno de sus 32.768 abuelos y abuelas.
Y si fuésemos capaces de encontrar la información necesaria para llegar a la trigésimo cuarta generación, nos encontraríamos con más abuelos que habitantes tiene la tierra actualmente.